- Autore admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:23.
- Ultima modifica 2025-01-23 15:31.

Esempi della sezione aurea possono essere trovati ovunque nell'architettura classica, nelle opere d'arte, nella natura e persino nella musica. Questa espressione di proporzione, nota anche come Rapporto Divino, offre una composizione armoniosa attraverso l'applicazione di un numero irrazionale (1.618) nel design, sia naturale che artificiale. Molto probabilmente, non sei a conoscenza dei calcoli dietro la bellezza della sezione aurea perché produce oggetti e musica che troverai naturalmente piacevoli senza bisogno di alcuna spiegazione.
Sezione aurea in architettura
La sezione aurea crea una bellezza quasi perfetta nella natura e nell'arte. Quando inizi a cercare esempi di sezione aurea nella vita di tutti i giorni, potresti rimanere sorpreso dai molti casi in cui è stata utilizzata per creare molti edifici e strutture monumentali. Quando la sezione aurea viene utilizzata in architettura, si dice che l'edificio sia stato creato utilizzando "architettura sacra". Applicando il calcolo della sezione aurea a un quadrato, architetti e designer sono in grado di creare il rettangolo aureo, che si ritiene abbia le proporzioni esteticamente più gradevoli all'occhio umano.
Esempio di rettangolo dorato: il Partenone

Fidia, lo scultore greco, usò la sezione aurea nel suo lavoro, soprattutto quando iniziò a lavorare con le fasce che scolpì appena sopra le colonne del Partenone. È anche importante notare che il valore numerico assegnato alla sezione aurea, Phi, è stato chiamato in suo onore.
Se misuri le dimensioni dell'esterno del Partenone, scoprirai che non solo forma un rettangolo d'oro, ma che ci sono anche molti rettangoli d'oro tra le colonne. Questa struttura sacra è un bellissimo esempio della sezione aurea in architettura.
Esempio del Triangolo d'Oro: Grande Piramide di Giza
La sezione aurea, il rettangolo aureo e il triangolo aureo si trovano tutti nella perfezione di una delle sette meraviglie del mondo, la Grande Piramide di Giza. Per trovare la sezione aurea, dovrai dimezzare la base quadrata della piramide e tracciare una linea verticale al centro della piramide. Quando questo è collegato a un lato angolato della piramide, puoi facilmente vedere come forma un triangolo d'oro con un rapporto di 1,618, la sezione aurea.
Altri esempi architettonici
Puoi trovare molti esempi di architettura sacra antica e moderna e di edifici in sezione aurea.
- Cattedrale di Chartres - Centro, Francia
- Notre Dame - Parigi, Francia
- Portico delle Fanciulle - Acropoli, Atene
- Taj Mahal - Agra, India
- Palazzo delle Nazioni Unite - New York, New York
Sezione aurea negli esempi artistici
Puoi trovare molti esempi di maestri pittori che hanno utilizzato la sezione aurea. Queste opere di perfezione sono state create utilizzando il rapporto tra rettangoli dorati e triangoli dorati. L'arte creata sulla base del rettangolo dorato si rivela più gradevole all'occhio umano. È uno dei misteri che circondano il rettangolo perfetto e la sezione aurea.
Sezione aurea nell'arte

Esempi artistici della sezione aurea includono:
- Leonardo Di Vinci - Monna Lisa, Uomo Vitruviano
- Botticelli - Nascita di Venere
- Michelangelo - Sacra Famiglia, 'David'
- Raffaello - Crocifissione
- Rembrandt - Autoritratto
- Salvador Dalì - Il sacramento dell'Ultima Cena, La persistenza della memoria
Utilizzo della sezione aurea nella composizione artistica
All'interno di un rettangolo dorato ci sono alcune aree che risultano visivamente più attraenti rispetto ad altre aree. Questi punti si scoprono tracciando una linea dall'angolo inferiore del rettangolo all'angolo opposto e ripetendola con l' altro angolo inferiore. Queste linee si intersecheranno al centro esatto del rettangolo d'oro. Successivamente, misura la metà di ciascuna linea partendo dal punto centrale. Questi quattro punti sono chiamati gli occhi del rettangolo (sezione aurea). Il punto focale principale del dipinto viene quindi disegnato o dipinto all'interno di questi punti di interesse (rapporti).
Sezione aurea nella musica

La musica è composta da valori numerici e quando la sezione aurea viene utilizzata per creare un brano musicale, diventa un esempio vivente di matematica. La sequenza di Fibonacci è prevalente anche nella musica:
- Ci sono otto note in una scala.
- La terza e la quinta nota sono la base degli accordi.
- La lunghezza, o ottava, di qualsiasi nota è di 13 note.
La sequenza continua durante tutto il brano musicale e diventa più complessa quando raggiunge la sezione aurea.
Compositori che hanno utilizzato la sezione aurea
Alcuni dei compositori classici più conosciuti hanno utilizzato la sezione aurea e la sequenza di Fibonacci nei loro brani musicali, tra cui Bach, Beethoven, Chopin e Mozart. Alcuni compositori moderni come Casey Mongoven hanno esplorato la sezione aurea nella loro musica.
Esempi di sezione aurea in natura

Dove si trova la sezione aurea in natura? È nella spirale aurea o di Fibonacci, che può essere creata utilizzando la sezione aurea. Questo è un fenomeno che si trova ampiamente nel mondo naturale. Le foglie di una pianta crescono in modo che quante più foglie possibile possano risalire a spirale lungo lo stelo. Una nuova foglia si forma solo dopo che si è formata quella che la precede.
- Cactus a spirale
- Galassie a spirale
- Girasoli
Fiori con la sequenza di Fibonacci
Alcuni fiori hanno petali che seguono la sequenza di Fibonacci:
- Tre petali:Iris, giglio, orchidee, trillium
- Cinque petali: Ranuncoli, gerani, ibisco, ipomea, nasturzio
- Otto petali: Delphinium
- 13 petali: Alcune varietà di margherite, erba tossica, calendula
Spirale di Fibonacci nelle pigne

A seconda della specie di albero, puoi anche vedere la sezione aurea all'opera all'interno di una serie di numeri di Fibonacci nelle pigne. Puoi trovare una serie di otto spirali su un lato della pigna, con 13 spirali sull' altro. Un altro motivo a pigna ha cinque spirali su un lato e otto sull' altro.
Sezione aurea negli esseri umani
Questo rapporto è importante non solo per il modo in cui gli esseri umani si vedono l'un l' altro, ma anche per il modo in cui funzionano i loro corpi e per il loro DNA.
Il DNA rivela la sezione aurea
Uno degli esempi più sorprendenti di sezione aurea si trova all'interno della struttura del DNA umano. Questo può essere visto in una singola sezione trasversale del DNA che rivela che la doppia elica del DNA forma una forma decagonale. Questa è una combinazione di due pentagoni, ruotati di 36 gradi l'uno dall' altro, forma la doppia elica del DNA. La stessa spirale a doppia elica forma un pentagono. Anche una singola molecola di DNA rivela una base della Sezione Aurea o Proporzione Divina.
La matematica dietro la sezione aurea
Trovare la sezione aurea nella vita reale è semplice, poiché appare ovunque intorno a te. È una verità matematica utilizzata per definire quello che è comunemente noto come il numero perfetto presente in natura e che è stato duplicato e imitato dagli esseri umani per secoli. La bellezza semplicistica di questo numero nasconde la sua complessità nell'esecuzione. Per comprendere la teoria alla base della sezione aurea, devi prima esplorare la sequenza di Fibonacci della sezione.
Sequenza di Fibonacci e sezione aurea
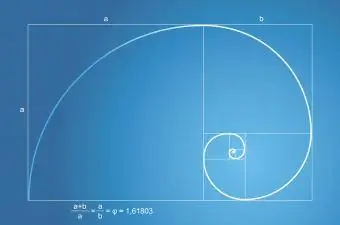
La sequenza o serie di Fibonacci ha una relazione con la sezione aurea. La serie di Fibonacci si manifesta nel numero di foglie su una pianta e nel numero di petali su un fiore. La spirale di Fibonacci, che si trova in natura, fa sempre parte di un rettangolo aureo con una sezione aurea.
La matematica della serie di Fibonacci è semplice:
- La sequenza inizia con 0 e 1.
- Basta sommare gli ultimi due numeri per ottenere il numero successivo della serie.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 e così via.
- Questo esempio della serie di Fibonacci diventa: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 e così via.
La relazione tra Fibonacci e la sezione aurea si realizza quando questa viene aggiunta in avanti, ulteriormente e ulteriormente. Più aggiungi le serie, più ti avvicini alla sezione aurea.
Creare un rettangolo e un triangolo dorati
Per creare un rettangolo aureo con la sequenza di Fibonacci, inizi con un quadrato. Inizierai a costruire un rettangolo aggiungendo un altro quadrato al quadrato originale. Ricorda di usare la formula: 0+1=1 è il primo quadrato, 1+1=2 - aggiungerai un altro quadrato.1+2=3 aggiungerai tre quadrati e successivamente, 2+3=5, aggiungerai cinque quadrati. Continuerai ad aggiungere quadrati e alla fine formerai un rettangolo dorato.
Un triangolo d'oro può essere creato dividendo in due un rettangolo d'oro da un angolo all'angolo opposto. Questo crea un triangolo in cui i suoi tre lati o angoli hanno una proporzione 2:2:1, il che significa che i due lati lunghi sono uguali in lunghezza e l'angolo corto è esattamente la metà della lunghezza dei due più lunghi.
Sezione aurea nel mondo reale
La sezione aurea viene spesso definita sezione divina a causa della sua importanza nella natura e nei corpi umani. La scoperta che la sezione aurea è presente in così tanti esseri viventi ha alimentato una venerazione per questa proporzione magica, che continua a essere fonte d'ispirazione per artisti e creatori oggi.






